멋쟁이사자처럼 AI스쿨 기초 통계 강의 내용을 정리한 포스팅입니다.
[1교시]
Q.통계를 왜 배워야 하나?
- 전문가 판단보다 낫기 때문에 (일관성이 높음)
[전문가 판단 vs. 통계적 예측]
- 임상적 예측 대 통계적 예측 : 증거의 이론적 분석과 검토 / Paul Meehl (1954년) / 통계적 예측이 더 정확하다.
-그로브 등 136개 연구에서 통계적 예측이 더 정확
-루이스 골드버그 : 전문가를 예측하는 모형이 전문가 자신보다 정확
-통계적 모델 (전문가가 내린 판단을 예측) 연구
-전문가의 판단은 내부적, 외부적 잡음 (전문가의 능력을 떨어뜨림)에 영향을 받는다. / 비일관성
ex) 네이버에 합격할지 예측하는 모형 : 통계 예측으로는 합격해야 하는데, 면접관은 불합격을 줌, 실제로 일을 할 때는 일을 잘 함.
-전문가의 판단을 예측하는 통계적 모델은 잡음에 영향을 받지 않는다.
ex) 이스라엘 연구 : 가석방 승인률이 점심시간 전에는 낮고, 점심시간 이후에 높아짐
-마틴 유 & 네이선 컨슬 : 무작위 공식도 대부분 전문가 판단보다 선발을 잘 한다.
ex) 판사의 판결, 채용 면접 등...
-로빈 도스 : 단순 합이 대부분 전문가 판단보다 낫다.
2.쉽게 복사해서 가져다 쓸 수 있다.
-요즘 AI는 통계와 밀접한 관련이 있음.
그럼에도 불구하고...
[왜 통계적 예측은 충분히 사용되지 않는가?]
-타당성의 환상 : 스스로 생각하는 판단의 정확성과 실제 정확성의 괴리
ex) 면접, 채용 (내가 안목이 있다는 자신감) : 잘 뽑았는지 못 뽑았는지 나중에 학습이 일어나지 않음..ㅠㅠ
-판단을 직접 내릴 때 얻는 만족감(퍼즐이 맞춰지는 느낌)이 보상으로 작용
-통계적 지식의 부족과 반감 (통계 잘 모름..)
-통계가 완벽하기를 기대하고, 오류에 지나치게 실망함. 반면 인간의 실수에는 관대함
ex) 그림그리는 AI -> 왜 이것도 못그려 ??
-예측에서 단순성과 복잡성에 대한 오해
ex) 복잡하게 봐야 예측을 잘 할 수 있다 ? (면접 때 목소리, 표정, 제스처, 복장 등 모두 봐야하지 않나)
오히려 너무 많은 변수들로 혼란스러울 수 있음
통계로 할 수 있는 것?
[대상의 특성을 수치로 표현하기]
-대상의 관찰할 수 있는 특성은 무엇이든 수치로 표현할 수 있다
-양적인 것, 질적인 특성도 수치화가 가능
-수치가 객관적이지 않아도 된다 (만족도 -> 별점)
[부분을 통해 전체를 추측하기]
-부분을 통해 전체를 합리적으로 추측하는 것이 중요함
-일부만 관찰할 수 있기 때문
ex) 여론조사, 면접(개인의 한 순간만 조사)
-현실에서 불확실성이 존재함
[비교하기]
-A가 낫나? B가 낫나?
[예측하기]
-주택 매매시, 얼마에 거래가 될까? (입지, 교통, 환경 등 파악 + 가격은 거래 과정에서 파악)
-미래에 대한 예측만을 의미하는 것은 아님
[영향력을 미치는 변수 찾기]
-대상의 한 가지 특성은 여러 특성으로부터 영향을 받음
ex) 고객 만족도 : 가격, 친절한 서비스, 경쟁 서비스 등에 영향
ex) APPLE : 가격에 영향을 받지 않는 모습.
[지수(index) 만들기]
-직접 관찰하기 어려운 대상의 특성 -> 관찰 가능한 다른 특성과 연관이 있음
ex) 고객 만족도가 높으면 재구매, 추천 등 행동을 많이 한다.
-관찰 가능한 특성들을 바탕으로 지표화할해서 통계적으로 다룰 수 있음
[비슷한 것끼리 모으기]
-비슷한 것들을 하나의 집단으로 인식 (물리적 차원 외)
ex) 홍대,합정 하나의 상권 / 신촌은 다른 상권
[2교시]
Q. 통계는 왜 어려운가 !?
-통계학은 학문으로 매우 늦게 형성되었다. (1911년에 영국 UCL에서 통계학과가 설립됨)
-인류의 자연스러운 사고방식과는 동떨어짐
-많은 계산이 필요하고, 초기 통계학 형성될 때 현대적 컴퓨터가 없었음 -> 손으로 쉽게 계산할 수 있는 형태의 방법론이 발전함 -> 이해하기 쉽지만 손으로 계산하기 어려운 것은 발전되지 않음
-통계학 개념들은 일상적, 직관적 관점에서 이해가 어려움
-직관적 관점에서 이해하지 말고, 통계적 관점을 수용할 필요가 있음
ex) 한국인 관점에서 외국 음식을 한식처럼 먹으려고 하면... ㅠㅠ 느끼한데 김치없이 어떻게 먹어??
외국에는 느끼하다는 틀이 없음... 아... 통계학자들은 이렇게 생각하는구나라고 받아들이기 ㅋㅋ
[이상한 통계학 용어]
-번역이 이상한 경우 : 모수
(엄마, 분모와 관련 없음)
-역사적 과정을 거쳐서 의미가 변함 : 회귀분석
(돌아가는 것과 직접적 관련 없음)
-만든 사람들의 사고 방식이 특이한 경우 : 통계적 가설 검정
(과학 가설 검정과 다른 철학적 관점을 가짐 / 실증주의 vs. 반증주의)
=> 용어를 보고 뜻을 대충 짐작하면 안 된다 !!!
[본격적인 통계 강의]
1.변수의 종류
(1) 데이터 표로 정리하기 (관행적으로)
-행(row) : 가로 방향 / 하나의 사례
-열(column) : 세로 방향 / 하나의 변수
(2) 범주형 변수 (categorical variable)
-ex) 주거 형태 (자가, 임대) / 고향 / 학력 / 출석 / 국적
-종류, 이름 등에 해당
-숫자로 표시해도 양적인 개념이 아니고, 대부분 연산이 의미가 없음
-순서가 있을 수도 있지만, 간격이 일정하지 않음
(3) 연속형 변수 (continuous variable)
-ex) 무게, 나이, 시간, 거리, 자녀의 수, 시험 점수
-간격이 일정하고 덧셈,뺄셈 등의 양적인 계산이 의미가 있다.
Q. 만족도는?
-엄격하게 따지면 서열변수(불만족, 보통, 만족) -> 범주형 변수로 보나,
-실무적으로는 별점을 평균내는 것처럼 연속형으로 보고 처리하는 경우가 많음
(가능하면 연속형으로 씀)
2.데이터모으기
(1) 데이터 모으는 방법
-공공 데이터
-인터넷 스크래핑
-기업 등 내부 자료
-설문
-관찰
-실험
Q. 설문보다 기계로 측정한 데이터가 더 낫지 않나?
-MRI로 뇌를 찍어서 분석을 해줌 (지능, 성격, 적성...) vs. IQ테스트
-MRI는 측정할 때마다 결과가 조금씩 다르게 찍힘
-IQ테스트도 검사할 때마다 결과가 다르나, MRI보다 신뢰도가 높게 나옴
-기계로 측정하면 신뢰도는 높지만, 타당도가 높다고 할 수 없음
(2) 타당도와 신뢰도
-타당도(validity) : 측정하고자 하는 것을 잘 측정함
-신뢰도(reliability) : 측정 결과가 일정함
-신뢰도가 낮다는 건 믿을 수 없다는 게 아니라 결과가 왔다갔다한다는 의미
-ex) 논술시험이 객관식보다 깊이 있는 이해를 했냐는 타당도가 높으나, 채점하는 사람에 따라 점수가 달라져서 신뢰도는 낮음
타당도를 정확히 알기 어려운 경우가 많음(극단적인 경우 재판) -> 신뢰도라도 높아야 함.
타당도를 알 수는 있는데 비용이 너무 큰 경우 -> 타당도를 어느 정도 양보
신뢰도가 낮은 경우가 도움이 될 수도 있다.
타당도 높은데 신뢰도 낮으면 측정 반복해서 많이 하기
반대의 경우는 방법 자체를 바꿔야 함 (객관식 문제, 찍어서 맞추는 경우 배제할 수 없음)
2.통계 분석의 도구
(1) 엑셀 : 최대 1백만행, 1만 6천열 크기의 데이터만 열 수 있는 한계
(2) R : 통계 분석을 위한 언어
(3) Python : 범용 프로그래밍 언어 (머신러닝, 인공지능에서 사용)
[확률 분포 (probability distribution)]
(1) 의미 : 확률 변수가 특정한 값을 가질 확률을 나타내는 함수
-이산(discrete) 확률분포 : 가질 수 있는 값이 정수
-연속(continuous) 확률분포 : 가질 수 있는 값이 실수
(2) 특징
-통계학의 근본 가정 중 하나
-무한한 확률 분포가 존재
-분석을 쉽게 하기 위해서 수학적으로 단순화, 추상화된 확률 분포들을 많이 사용
[베르누이 분포]
베르누이 분포
동전 던지기 같이 둘 중에 한 가지 결과만 나올 수 있는 경우
이항 분포
0과 1만 나오는 시행을 n번했을 때 합계의 분포
-여러 시나리오에서 자주 쓰임
-매장 계산대에 임계점 넘어서서, 갑자기 밀리는 현상있을 때
-고객 구매율이 30%일 때, 100명의 고객이 방문하면 그 중에 몇 명이 구매하나?
#binom은 이항분포 관련
from scipy.stats import binom
#pyplot 시각화 모듈
import matplotlib.pyplot as plt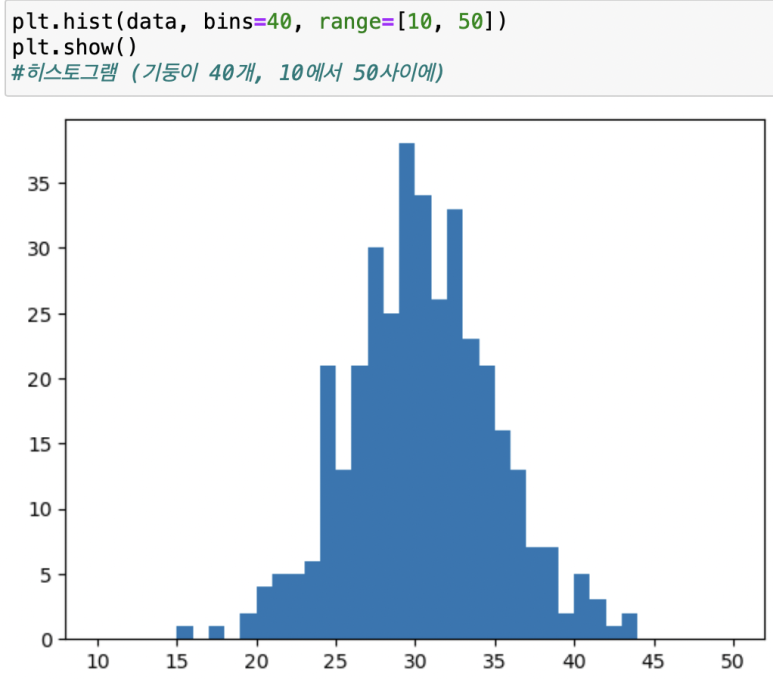
->1년동안 대략 45명까지는 커버가 가능하겠구나. 시뮬레이션을 돌려볼 수 있다.
카카오톡 서버 10,000개 (항상 일정해야 하는 값)
다운될 확률 1%
장애가 없이 운영되려면
#고장이 200대 이내로 발생할 확률, 1년중에 몇번이나 발생할까?
binom.cdf(k=200, n=10000, p=0.01)
#80대를 팔면?
binom.cdf(k=120, n=9920, p=0.01)
#60대를 팔면?
binom.cdf(k=140, n=9940, p=0.01)[이항분포의 확률질량함수와 누적분포함수]
확률질량함수(probabillity mass)
누적
[정규 분포 (normal distribution)]
-normal은 정상, 정규적인 것과는 무관하다
-가우시안 분포라고도 함
중심극한정리
ex) 6면체 주사위 20개를 던졌을 때,
주사위 하나 하나는 1부터 6까지 골고루 나오는데, 그 합계는 대략 70 언저리에서 몰려서 나옴
합계도 20~120까지 고르게 나오지 않음
[통계의 종류]
기술 통계 (descriptive statics) :테크닉이 아니라, 묘사하다 기술하다의 기술...
(1)중심 경향치
-평균 (mean)
: 극단값에 따라 영향을 크게 받음 (해석할 때 주의가 필요하다)
ex) 10, 20, 30, 40, 50 -> 30
10, 20, 30, 40, 500 -> 120
: 고객당 평균 구매액수 * 고객수 = 매출로 예측할 때 유용
-중간값 (median)
:중위수라고 표현하기도 함
: 값들을 크기 순으로 정렬했을 때 중간에 위치한 값
ex) 10, 20, 30, 40, 50 -> 30
10, 20, 30, 40, 500 -> 30
:극단값에 영향을 받지 않는 장점이 있음
청소년 첫 성경험 평균 나이...?
-> 평균으로 의미가 없다... (해당 안 되는 경우가 더 많고... 해당 안되었다가 된 경우에 따라 평균이 매번 달ㄹ라지는 것도... 유의미한 정보가 되지 않음)
-> 청소년 중에 1% 해당, 평균 나이 13세 (A국)
-> 청소년 중에 50% 해당, 평균 나이 14세 (B국)
-> 나이별 비율이 차라리 주는 정보다 더 많다.
ex) 첫 취업 평균 나이
Q. 퇴직 평균 연령의 경우는?
-> 퇴직은 언젠가는 하니까 통계에서 빠지지 않으니,
-> 비슷하게 평균 수명도 언젠가는 죽음을 맞이하니까 (좀더 정확한 정보는 연령별 생존률??)
[분위수 (quantile)]
-크기순으로 정렬된 데이터를 q개로 나누는(분) 위치의 값
-ex) 사분위수, 백분위수
-사분위수(quartile) : 데이터를 4등분하는 위치 (교과서적으로 많이 쓰임, 좌우 대칭 비교하기 편해서)
-백분위수(percentile) : 데이터에서 순위를 퍼센트로 표현 / 10percentile은 위치로 말할 때, 10%까지 구간을 의미
[범위]
max, min : 일상적 의미의 범위
max - min : 통계적 의미의 범위
df.price.max() - df.price.min()IQR(InterQuartile Range) : 사분위간 범위
df.price.quantile(.75) - df.price.quantile(.25)상자 수염 그림 (box-whisker plot)
-1~3사분위수를 상자로 표현하고, 최솟값과 최댓값은 수염으로 표시
-수염의 최대 길이는 IQR의 1.5배까지, 넘어가면 ...(점)으로 표시
[분산과 표준편차]
분산 : 절대값을 씌우지 않고, 제곱하는 이유는 수학적인 의미가 있음.
표준편차 : 분산에 루트 씌움
표준화시키기
cf) 샤프지수 (예금, 주식, 코인의 투자수익률 비교... 위험을 고려해서 표현) = 투자수익률 / 위험 표준편차
df.mileage.var()
df.mileage.std()[히스토그램]
sns.histplot(x='price', data=df, bins=30)
#막대기 특정 구간에 걸리게 지정하기
sns.histplot(x='price', data=df, bins=[0, 500, 1000, 1500, 2000, 2500])
#반복문으로 구간 설정
xs = list(range(200, 2100, 200))
sns.histplot(x='price', data=df, bins=xs)
plt.xticks(xs)[커널 밀도 추정]
: 데이터의 밀도를 추정하여 그린 곡선
ex) 가격 측정할 때, 1000만원 1500만원 잘 매기는데, 1220만원 이런 가격대는 매기지 않는 경우도 있음
sns.histplot(x='price', data=df, bins=30, kde=True)[모집단과 표본]
모집단(population) : 연구 관심이 되는 집단 전체
-모집단은 다 관찰할 수 없음 (대부분 전수조사가 불가함)
-우리가 만날 일이 없다. (항상 보는 건 표본임)
ex) 고객 만족도의 모집단은 모든 고객 (아직까지 구매하지 않은 예비 고객도 포함)
표본(sample) : 특정 연구에서 선택된 모집단의 부분 집합
-고객 1명이 아니고, 고객 무더기가 하나의 표본임
표집(sampling) : 표본 추출 (모집단에서 표본을 추출하는 절차)
[모수 (population parameter) : 모집단의 특성치]
parameter : 어떤 시스템의 특성을 나타내는 값
population parameter : 모집단의 특성을 나타내는 값
-ex) 모집단의 평균, 모집단의 분산
-모수가 적다, 많다는 틀린 표현이 나옴 (표본의 크기를 모수라고 잘못 표현)
[통계량 (sample statistic)]
표본에서 얻어진 수로 계산한 값 (=통계치)
추론 통계 : 표본 통계량을 일반화하여 모집단에 대해 추론하는 것
'데이터 사이언스 스터디 > 통계' 카테고리의 다른 글
| [데이터 분석 통계] A/B Test Summary (0) | 2024.12.11 |
|---|---|
| 데이터분석을 위한 기초 통계3 (3) | 2024.12.11 |
| 데이터분석을 위한 기초 통계2 (2) | 2024.12.11 |